パラメータベクトルを用いた、フェルマー・ワイルズの最終定理に対する考察(3)
- S Y
- 2023年1月31日
- 読了時間: 4分
0.参考文献
[1]
[2]
[3]
1.ラグランジュの未定乗数法[3]
詳細は説明しませんが、制約関数gのもと、ある関数fを最大化、あるいは最小化したいとした時、ラグランジュの未定乗数法により、最大値を求めることができます。
このことは、結局、ある関数fの停留点を求めることに似ています。

今回は、パラメータベクトルによる微分を何階か行い、これらをラグランジュの未定乗数法により接続した関数Lについての停留点を考察します。
2.n=1の時(x+y=z)
変数は3つあるので、パラメータベクトルは2変数t=(m,n)とします。
この時、次のように計算できます。
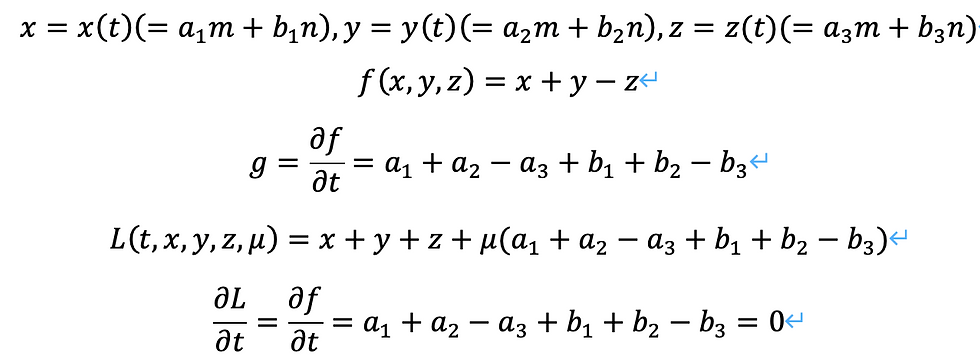
結局、パラメータの係数に対して、同じ問題を与えることとなりました。
これはすなわち、線形性のある空間全体が解集合となることを意味します。だから、自然数が解空間となるわけです。
3.n=2の時(x^2+y^2=z^2)
n=1の時と同様に考えます。
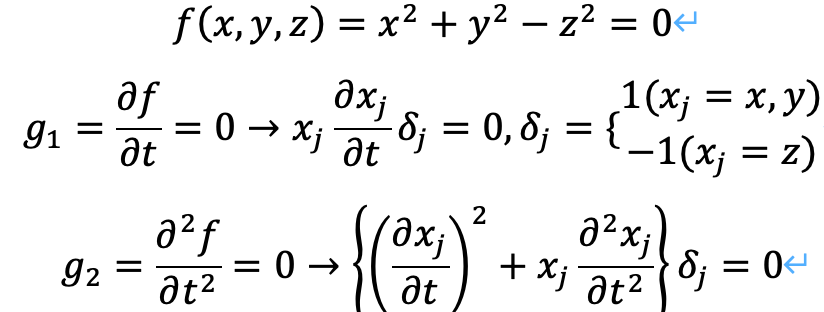

特に、x_j=xの時、正負、0の対称性も考えると、次のように考えることができます。
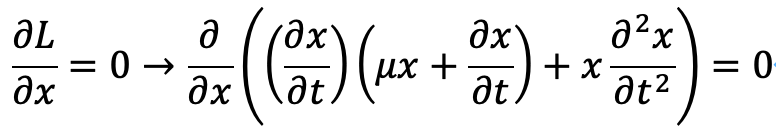
以上を整理すると、次のようになります。
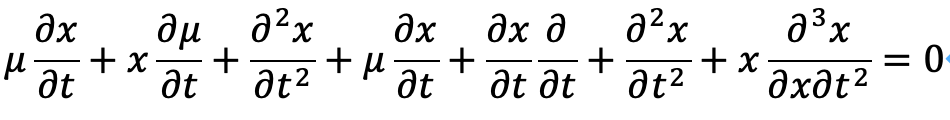
右から、∂t/∂x倍し、整理します。

μについての微分方程式となります。斉次解は次のようになります。
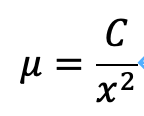
定数変化法を用いることで、C=C(x)について考えます。

これを解けば、次のようにもとまります。

以上から、一般解は、次のように得られます。
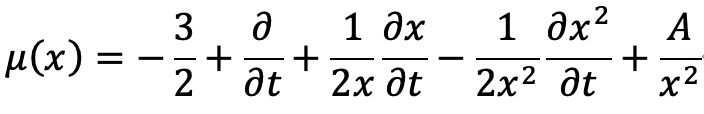
この特異点はx=0です。特異点が一つ存在することがわかりました。
4. n=3の時(x^3+y^3=z^3)
関数f(x,y,z)=x^3+y^3-z^3について、パラメータ微分を行います。また、ラグランジュの未定乗数法を用いることで、Lを求めることができます。

ここで、Lをxで微分するときに、y,zを消去できることを使いました。
また、g_1, g_2について、ある種の拘束条件、g_3がある種の運動であると捉えることで、ラグラジアンを考えました。
ところで、ラグラジアンのx微分は、最小作用の原理から0となるはずです。

μ1とμ2について、それぞれの斉次方程式はこのようになります。
それぞれ、次のように微分方程式を解くことができます。
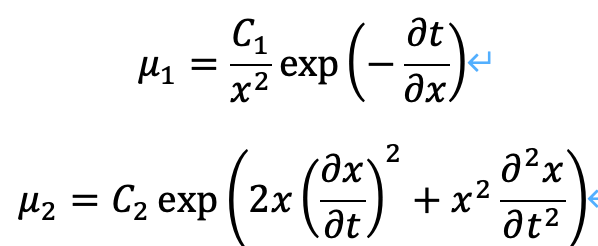
以上を、μの2種の解であると捉えることとします。
これらを定数変化法を使って特殊解を求めることは、とても難しいので、ロンスキアンを使って考えることとします。
手始めに、μ1とμ2について、xで微分します。

未定乗数Cは一度無視して、次のようにします。

すると、ロンスキアンは次のようになります。
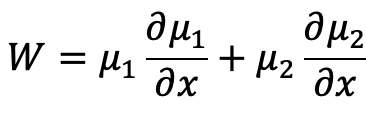
すなわち、μ=μ(μ1,μ2)は次のようになります。
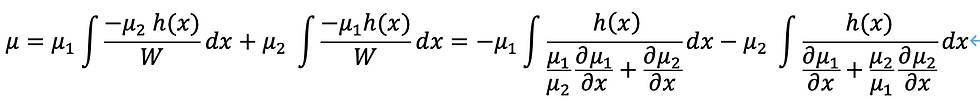
以上から、代入すれば次のようにもとまります。
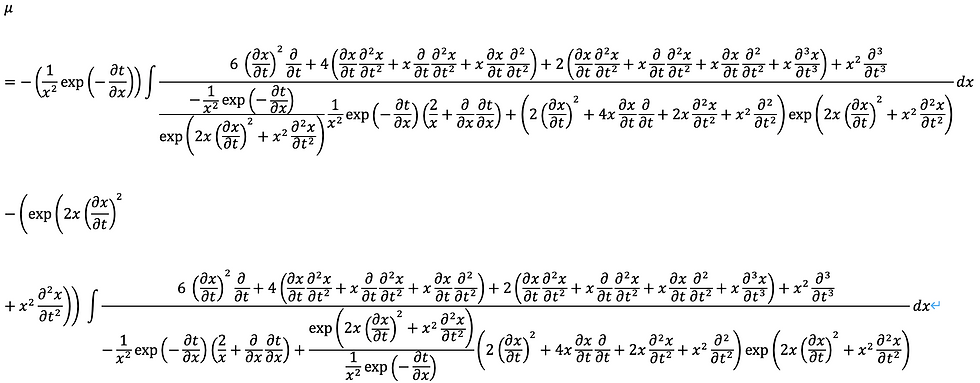
この特異点は、x^2=0、W=0となります。
W=0について、考察します。

特異点は、この方程式の解となります。
簡単のため、∂t/∂xなどを全て1であると仮定すれば、次のように書き換えることができます。
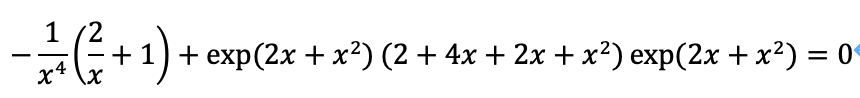
この解は計算機により求まり、次の結果を得ます。

重要なのは、特異点がx=0を含めると4つ存在することです。一つではないことです。
5.特異点の個数とパラメータベクトル
そもそも、パラメータベクトルが存在するとは、どういうことでしょうか?
まず、方程式の原始解空間を用意します。例えば、x^2+y^2=z^2を満足する原始解(x,y,z)全体を指します。
原始解空間は、いわば原始解という点を接続した線のような性質を持っていると考えられます。
ここで、実は原始解に対して、ある定数倍した解も、x^2+y^2=z^2を満足します。(フェルマー・ワイルズの最終定理でも、同様です)。
すなわち、ある原始解から定数倍することによって得られる集合もまた、解空間をなすこととなります。すなわち、面のような性質を持っていると考えられます。
つまり、解空間とは、ある意味で円筒のような形状をしているわけです。(円断面は、ある原子解とその定数倍からなる解空間、長方形断面は、原子解の集合)。
そして、円筒の長方形断面が最大となる時の、長方形の長い方の中線こそ、パラメータベクトルとなるわけです。
ところが、このパラメータベクトルが複数あるとすれば、言い換えると、特異点が複数あるとすれば、ある解空間に対して、「問題に対して適切であり、かつ不適である」という異常事態が生じてしまうわけです。
今、x^n+y^n=z^nという問題空間の解空間を考えるとき、この問題空間は一つでありながら、しかし一方で解空間は複数ある、という矛盾が生じてしまいます。
だから、nが3以上であれば、パラメータが存在しない=解は存在しないと言えるわけです。


コメント