パラメータベクトルを用いた、フェルマー・ワイルズの最終定理に対する考察(2)
- S Y
- 2023年1月28日
- 読了時間: 4分
0.参考文献
[1]
[2]
1.フェルマー・ワイルズの最終定理に関する追加情報[1]
フェルマー・ワイルズの最終定理とは、次の問題でした。

実は、nについて、素数だけ考えたら良いということが知られています。これを追加情報として連絡します。
そこで、フェルマー・ワイルズの最終定理は、次のように言い換えることができます。

「自然数x,y,zなる組み合わせで、nが奇素数である時、x^n+y^n=z^nを満足するものはない。」
2.n=3のとき
次の関数を考えます。
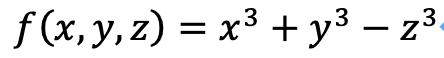
ここで、x=x(t)=x(m,n), y=y(t)=y(m,n), z=z(t)=z(m,n)とします。そこで、tで微分することとします。

これらは全て、0となるはずです。
3.正の数、負の数、0という対称性
0とは、ベクトルを考えた時、基準点、すなわち原点を意味します。そこからある値(絶対値)を考えた時、これだけ基準点から離れることを考えます。1次元を仮定すれば、これは2つの取り方があり、正の数、負の数が生じるわけです。
ところで、f(x,y,z)=x^n+y^n-z^nにおいて、負の数の候補はzだけです。唯一、-1倍されているためです。すると、xとyについては、いずれかを正の数と捉えたら、他方は0であることが推測できます。
実際、n=2の時は、以下のようになっていました。


以上から、次の推測ができます。

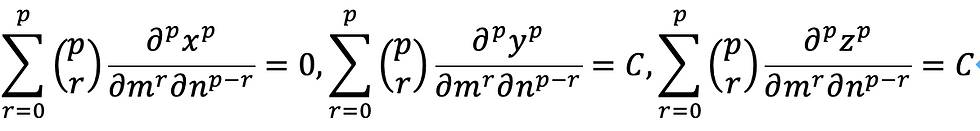
つまり、xについて、パラメータベクトルで微分すれば、それは0となり、y,zについては同じ定数となると推測したわけです。
特に、C=2pとなるだろうとも、予想することができます。(p=2の時、2p=4になっていますね。)
4.p=3のとき
4.1 準備
では、手始めに、奇素数の中で最も小さい数である、p=3の時について考察していきます。
2章の結果から、次の推測ができます。(推測A)
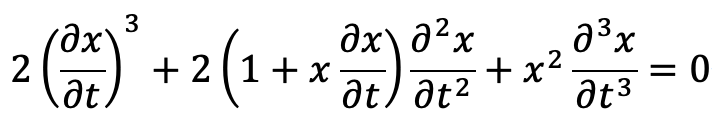
さらに、パラメータt=(m,n)のもと、xをmとnで次のように表せると考えます。ただし、mとnは互いに素であるとします。すると、原始パラメータとなります。

この時、1階微分、2階微分、3階微分については、次のように求めることができます。
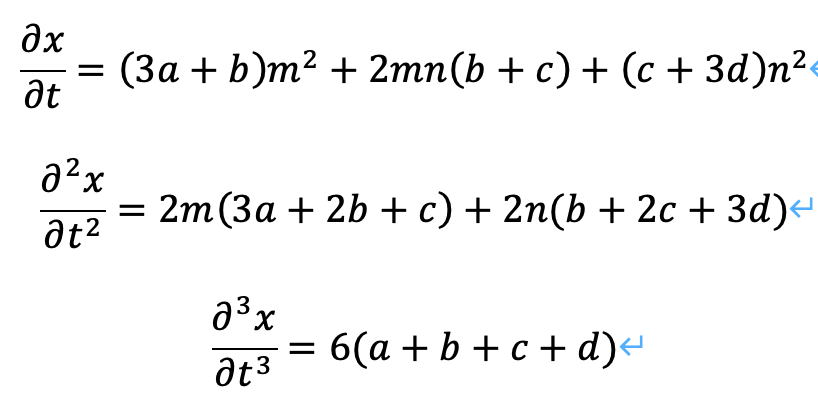
以上から、mとnを用いて、推測Aは次のように書き換えることができます。

第一項をパートA、第二項をパートB、第三項をパートCとします。
第一項(パートA)について、簡単に展開すれば、次のようになります。

ここで、mとnに依存しない、すなわちa,b,c,dの4つの数に対して、どのような制限を与えることができるか考えます。そのため、m^6, n^6について着目します。
パートA、パートB、パートCについて、以下の係数となります。

また、m^3n^3についても考えると、第一項については、特に次のことを考慮すべきでしょう。

以上から、次の推測ができます。
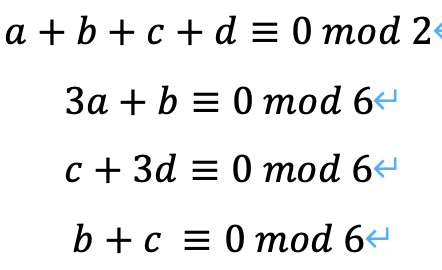
推測B
これで準備が完了しました。
4.2パターンI aとdが両方偶数と仮定
推測Bから、a+dが偶数であることがわかります。
そこで、aとdは、両方偶数か、両方奇数であることがわかります。
今回は、両方偶数であることを仮定します。
すると、bとcはいずれも6の倍数となることがわかります。
ところが、今回考えているのは原子パラメータt=(m,n)ですから、aからdに共通素因数はないと考えるべきでしょう。
すると、このパターンは間違っていると考えられます。
4.3 パターンII aとdが両方奇数と仮定
両方奇数であれば、aとdが互いに素である可能性が出てきます。すなわち、原始パラメータとして成立するというわけです。
この時、次の関係式が成り立つでしょう。

さて、m^6の係数について考えます。
直接代入すれば、次のようになります。

共通因子6(k+k')(2k+1)で割ることにより、次のように整理できます。
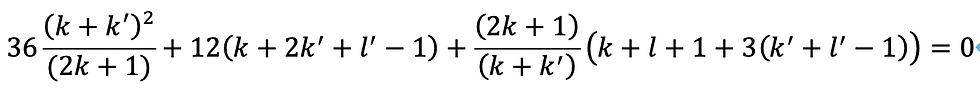
第一項と第三項を比較すれば、(k+k')^2/(2k+1)が整数で、かつ(2k+1)/(k+k')が整数であると考えるのが自然です。
すると、容易にk=k'-1という関係が得られます。
以上を整理すれば、次のようになります。
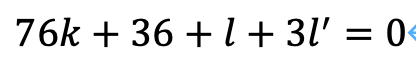
36の因数は2と3ですから、l=l'と仮定すればうまくいくことがわかります。
ところが、正負を考えると明らかにおかしいですし、これを仮定すれば、k=0.5となりますから、間違いとなることがわかります。
4.4 まとめ
p=3の時、うまくxを成立させるパラメータが存在しないことがわかりました。
そのため、p=3の時、フェルマー予想は正しいことがわかりました。
5.pが奇素数のとき
今回は次の関数を考えます。pは一般の奇素数です。

この時、パラメータ微分を考えます。

特にxについて、次の級数表現を考えることができます。

正負と0の対称性から、特に次の関係式を考えることができます。

この時、p=3の時と同様に、次の関係式があるだろうと推測します。
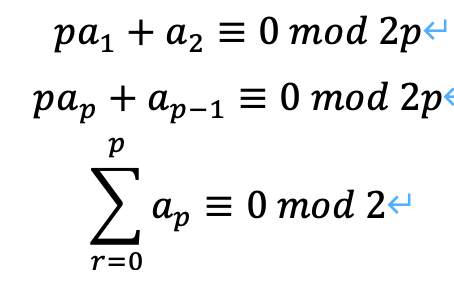
この結果から、次のように推測できます。

ここで、m^(2p)の係数を考えます。
整理すれば、次の結果を得ます。

これを代入すれば、以下の式を成り立たせる必要が出てきます。

この時、明らかにlとl'の正負から、この式は誤りであることがわかります。以上から、pが奇素数であるとき、一般にフェルマー・ワイルズの最終定理は成り立つことがわかりました。
結論、pが奇素数で成り立たないならば、一般の自然数(1と2を除く)に対しても同様に成り立たないので、nが3以上の自然数である時、フェルマー・ワイルズの最終定理は成り立つことがわかりました。


コメント