パラメータベクトルを用いた、フェルマー・ワイルズの最終定理に対する考察(1)

更新日：2023年1月26日

0.参考文献

[1]

[2]

1.フェルマー・ワイルズの最終定理[1]

nが3以上の自然数であるとすれば、x^n+y^n=z^nを成り立たせる自然数の組み合わせ(x,y,z)を与えることはできないとするものです。言い換えると、これを成り立たせるパラメータベクトルt, x=x(t)、y=y(t)、z=z(t)は存在しないという意味になります。

2.原子ピタゴラスの定理におけるパラメータベクトル表示[2]

自然数からなるパラメータt=(m,n)を用いて次のように定めると、任意の原子ピタゴラス数を与えることができます。

3.パラメータによる微分を定義する

次のような1*2行列を考えます。

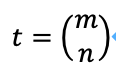
これがパラメータです。この時、次のことに気づきます。

微分した2つを合わせて2*2正方行列を考えると、これは単位行列になることがわかります。

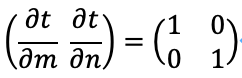
そこで、今まで(ある意味でベクトルを変数とみなした状態で)計算してきた、∂/∂tというのを、きちんとパラメータの側面から次元を上げることで、次のように定義することができることがわかります。

すると、最左辺は次のように書き換えることができるでしょう。

この事実をもとに、ベクトル微分を次のように表すこととします。

4.原子ピタゴラス数のパラメータt(m,n)による微分の結果と停留点に関する問題

2章で示した、原子ピタゴラス数のパラメータについて、パラメータ微分(ベクトル微分)をすれば、次のようになります。

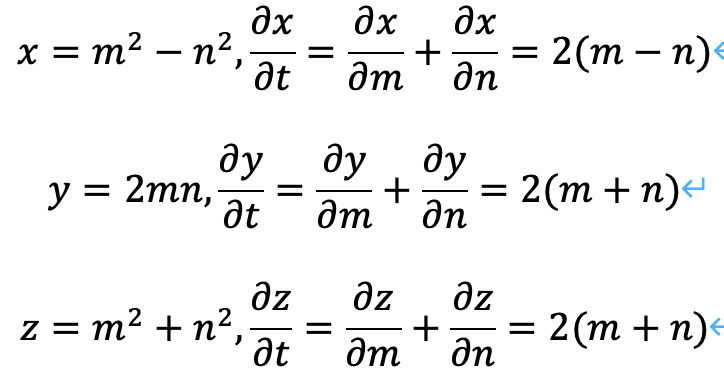
ここで、次の問題を考えます。

「任意の原子ピタゴラス数を与えるパラメータを導出せよ。このパラメータはただ一つであることも示せ。」

これは、次のように言い換えられるでしょう。

「関数f(x,y,z)=x^2+y^2-z^2の停留点かつ変曲点となるようにパラメータを与えよ。」

ある点が、停留点かつ変曲点であるとき、そこでは関数は定数ベクトルとなります。つまり、0か、定数となります。0となることを確かめるには、実際にパラメータを代入することでわかりますから、言い換えることができるのです。

そこで、原子ピタゴラス数について、実際に計算して確かめてみます。

まずは、停留点から考えます。

確かに、0となることがわかります。

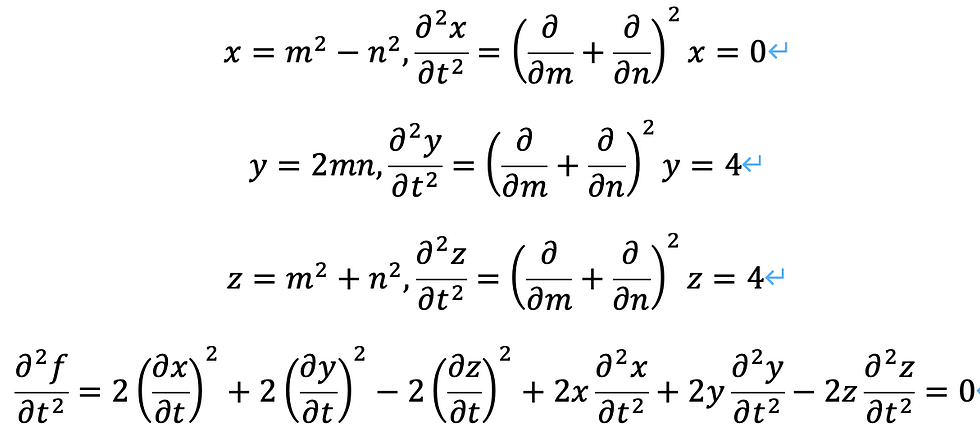
こっちも、確かに0となることがわかりました。

5.自然数x, yの線形和、z=x+yのzは自然数か？そのような(x,y,z)の組み合わせはどのくらいあるか？パラメータは必要か？

自然数は、ペアノの公理に従う数ですから、zも当然自然数となります。

これでは、パラメータに関して、よくわかりません。

まず、自由度は2ですから、パラメータの数は2つであることがわかります。また、パラメータの次元は、元の計算、z=x+yでは1次なので、最大1であることがわかります。以上から、次の数式を仮定します。

この時次のようにして、パラメータ微分を考えられます。

結局、文字が置き換わっただけで、同じ問題になります。すなわち、x+y=zを探そうとして、a1+a2=a3、b1+b2=b3を探そうとすることと同じになります。

2階微分は、a1, a2, a3、b1, b2, b3が定数ですから、0となります。

以上の結果より、パラメータは不要で、x,yが任意の自然数で良いことがわかりました。

次回は、3次の場合について考えます。

最新記事