ゴールドバッハ・オイラーの予想の証明

0. 参考文献

[1]http://www.tamagaki.com/math/Goldbach%27sConjecture.html　「ゴールドバッハ予想」

1. ゴールドバッハ・オイラーの予想とは

1742/6/7に、ゴールドバッハはオイラーに向けて次の手紙を送りました。

「5よりも大きい自然数は3つの素数の和で表せるだろう。」

これに対して、オイラーは次のように返しました。

「あなたの予想は、『４以上の偶数は２つの素数の和で表せるだろう』と言い換えられますね。」[1]

この説明は、参考文献[1]で詳細に説明されています。オイラーがいかに天才なのかがわかりますね。

さて、このような経緯で「４以上の偶数は２つの素数の和で表せるだろう」という、一般にゴールドバッハ予想が生まれました。同値の命題はゴールドバッハによって最初に与えられたものの、今知られている形のものはオイラーによってできたのですね。

2. 本日のオリンピック

日本史上最年少の金メダリストが誕生したり、その競技で日本人が1位と3位に入ったり、柔道では2連覇を達成したりと、素晴らしい成績でした！バスケットボールの3x3は数学者としては非常に気になりますね。ポジションや選手の能力によるポテンシャルエネルギーや、ボールに対する運動エネルギーなどについて考察したいです。

3. 証明

ゴールドバッハの予想によれば、任意の偶数

に対してある奇素数

が存在して、

が成り立ちます。これは次のような偶数

の存在を否定しています。(素数の2倍の偶数は、当然2つの素数の和で表せる。)

どのような奇素数

に対しても、次の等式を満たすために誤差

を必要とする、ある偶数

が存在して、次の等式の関係になります。

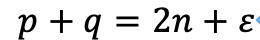
3.1 ε>0の場合

奇素数p,qに対し、ベルトラン・チェビシェフの定理を用います。

(nが偶数であるとき)

(nが奇数であるとき)

nの偶奇によらず、各辺をそれぞれ加えると、

等号成立は、

これはε>0に矛盾します。

等号成立はしないとしてもやはり、

となることより、明らかに矛盾します。

3.2 ε<0の場合

ε=-ε'を満たす、正の正数ε'>0を用いて、次のように書き換えます。

奇素数p,qに対し、ベルトラン・チェビシェフの定理を用います。

(nが偶数であるとき)

(nが奇数であるとき)

nの偶奇によらず、各辺をそれぞれ加えると、

最左辺と比較して、等号が成立するときは、

これはp+q=0となるので矛盾します。

等号成立はしないとしても、やはり

となることより、明らかに矛盾します。

3.3 まとめ

3.1, 3.2の結果より、ε=0。以上から次の結果が得られます。

この結果は、ゴールドバッハ・オイラー予想が正しいことを示しています。