Thoughts on the Lujandre Conjecture

0. References

[1] https://youtu.be/YNmRhCNvBbg The Lujandre Conjecture "University Mathematics and Physics" studied in a prep school atmosphere.

[2] https://www.chart.co.jp/subject/sugaku/suken_tsushin/91/91-4.pdf Using Bertrand Chebyshev's Theorem - Proof that n!(n>=2) is not a square number

1 What is the Lujandre conjecture?

It is the conjecture that for any natural number n, there will always be a prime number between n^2 and (n+1)^2. [1]

2 Bertrand Chebyshev's Theorem

It is a theorem that there is at least one prime number between n and 2n. [2]

3 Review of the Pythagorean number sequence generating equation

The Pythagorean number sequence generating equation, according to Tomatsumura, is as follows (Equation 1)

Now notice that the outlier is a^2. (Because the other two have dimension a^4.) For clarity, I shifted the right side and a^2 respectively, and replaced a^2 with n. (Equation 2)

Also, the following equation holds. (Equations 3,4,5)

4 Relationship between n^1 and n^2 classes

This is just a sensory thing. This is not proper mathematics, so please bear with me.

First, imagine the n^1 and n^2 classes of number lines separately. n^1 class is equally spaced 1,2,3,.... . n,n+1,n+2,.... . n,n+1,n+2,.... On the other hand, for the n^2 class, as n gets larger, the intervals get larger.

Now, for each number line, try connecting it with n and n^2.

Then, vector operations become possible on the lines connected to the number lines. By arranging the number lines well, you can also create right triangles.

Two parallel lines: n^2 class. By transforming the viewpoint coordinates, they have an intersection point at infinity.

Perpendicular lines: n^1 class.

Viewed from a plane. Parallel lines do not intersect.

A different point of view. There is a fixed infinity that is unique for each n. Intersections at infinity can be seen, for example, in one-point perspective in painting.

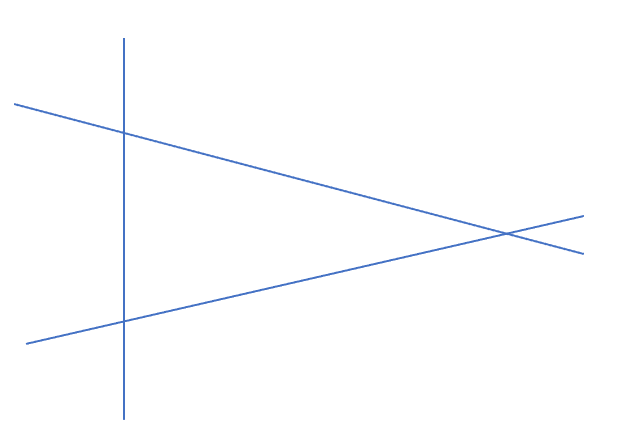
Since it is a Pythagorean number sequence generating equation, the triangle consisting of 4n and (n+1)^2, (n-1)^2 will be a right triangle, such that it corresponds to each n. So, it seems to be well-defined to make a right triangle by arranging the number lines well.

Somehow, I feel that the properties of the n^2 class and the n^1 class transformed by the Pythagorean number sequence generation formula are the same.

Now, from Bertrand Chebyshev's theorem, we know that there are at least two more primes between n and 4n: at least one from n to 2n, and at least one from 2n to 4n. In total, there will be at least two.

We can also divide the middle point, 2n, into n to 2n-1 and 2n+1 to 4n, since 2n is clearly not a prime number.

From this result, we can see that for the left-hand side of Equations 3 and 4, it would mean that there is one prime number in n→2n-1, which is equal to the vector n^2-(n-1)^2, and that there is one prime number in 2n+1→4n, which is equal to the vector (n+1)^2-n^2. This is the Lujandre conjecture.

This explains why the Lujandre conjecture is correct.

5 About not saying "proof".

I think it would be well-defined, but I didn't know the specific proof. Therefore, I only mentioned it here as an impression stop. Also, I didn't know the proof of whether the properties of the n^2 class are actually the same as those of the n^1 class.