Reflections on the predictions of Erdes Strauss (Part 1)

0. References

[1]https://picolinateu.hatenablog.com/entry/2016/09/13/132916

Erdes Strauss Conjecture 1 (Case-by-Case Method) - Mathematics Made Easy for Middle and High School Students

1 What is the Erdes-Strauss Conjecture?

It is Erdes Strauss's conjecture that the following proposition will be true. [1]

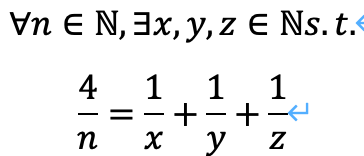
I made a conjecture that the following proposition, which is a development of this proposition, would be true. (Conjecture 2)

2 When m=3

Conjecture 2 is true when n=2, 3, or a prime of type 6s-1 and their multiples, or an even multiple of a prime of type 6s+1. (Conjecture 2 is true except when it is an odd multiple of a prime of type 6s+1.)

2.1 When n=2,3

This can be established by stipulating the following.

2.2 The Other Case

Let's assume that x_i contains a, and consider the other number.

Since the numerator is a divisor of the denominator and the numerator is a divisor of the denominator, we have the following relationship using the natural number t.

Solve for a.

Considering that we are approximating by n, and assuming that t is a multiple of n, and setting t=nu, we have

Furthermore, we assume that a=u and solve for u(=a).

If we set n=6s-1, then u=a=2s. If we set n=2(6s+1), then u=a=4s+1.

From the above, we know that Conjecture 2 is true when n=2, 3, or 6s-1 primes and their multiples, or even multiples of 6s+1 primes. (Conjecture 2 is correct except when it is an odd multiple of a prime of type 6s+1.)

3 When m>=3 (except when n is an odd multiple of a prime of type 6s+1)

We can make Conjecture 2 hold by adding 1/n to both sides (m-3) times.

To be continued.

4 Today's Olympics

Softball

You won! I think the good flow came to the Japanese side after they successfully got out of a pinch in the first inning!

Tennis

Women's Tennis

It was a close match. I wanted her to take the second game somehow and create a flow from there.

Men

Congratulations on winning the second round! Keep up the good work!

Surfing

Congratulations to both the men's and women's teams for winning medals!

Women's Soccer

Congratulations on making it through the first round!

3 on 3

It's been a while since I've been to Round One. It was very interesting to watch, and I would like to do some mathematical physics research on it someday.