Reflections on Erdes Strauss's predictions (Part 2)

1. review of previous article

We proved that the generalized conjecture of Erdes Strauss is correct when n=2, 3, or 6s-1 type primes and their multiples, or even multiples of 6s+1 type primes.

2. what we will consider this time & explanation

For a prime number n of type 6s+1, we consider the even odd of s.

If s=2t, 2t-1 (t>=1), then 6s+1=12t+1 and 12t-5 respectively.

First, let's consider 12t-5.

We can find that a=4t by calculating a=bu, b=5 in the following equation we considered last time.

From the above, it is

To summarize, we get the following equation

Next is 12t+1, again, this time for t, and consider its evenness.

If t=2g, 2g-1 (g>=1), then 12t+1=24g+1 and 24g-11 respectively.

First, we will consider 24g-11 in the same way.

In the same way, if we calculate a=bu and b=11, we find that a=8t.

The following equation holds.

To summarize, we get the following equation

3. discussion about 2

By successfully replacing s with 2t, we were able to make b an odd (prime) number of type 6s-1. This shows that there are multiple ways to represent, for example, 4/35.

We can also consider the case of

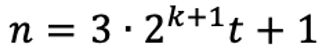
in the same way. Then we can see that it satisfies the following relation.

Again, suppose that n is a prime of type 6t+1 (synonymous with a prime of type 6s+1). Therefore, k=0. If we substitute, we get the following relation

To be continue...

4. today's Olympics

Women's Soccer

We lost to Sweden, unfortunately. I know it's very difficult, but if we had been able to score in the decisive moments, we might have won... I wanted us to win 4-3.

Men's Tennis

No way, Djokovic lost.... I'm shocked.

Men's Handball

It's a pity that he lost a close match.

Badminton mixed doubles

Congratulations on your bronze medal!

Fencing

Congratulations on your gold medal!

Judo

Congratulations on winning the gold medal!