Proof of the non-existence of perfect bricks

0. References

[1]https://www2.hamajima.co.jp/kyoto-math/pdf/kyomath202011.pdf　

Today's number: "44

"Today's Mathematics vol.44" Published November 2020 by Rakuhoku Arithmetic　

[2] https://en.wikipedia.org/wiki/Euler_brick

Euler brick - Wikipedia

[3] https://twitter.com/Stonesvoice1/status/1292293530979721216

Pythagorean number sequence generating equation

[4] https://manabitimes.jp/math/661

Formula for generating Pythagorean numbers

Euler's brick

A rectangular object whose sides and diagonals are all natural numbers is called an "Euler brick". For example, the smallest three sides are "44, 117, 240". In fact, we can see that the following formula holds [1]

This is known, among other things, to be a parameter display. Reference [2] explains it in detail.

2. unsolved problem

A perfect bricks is a bricks in which the lengths of the sides and diagonals of all the faces plus the diagonals of the bricks are natural numbers. The question of whether or not it exists is unsolved.

This means that in addition to the diagonals of each side (a, b, c) and each face (d, e, f), the diagonal of the rectangle g is also a natural number. The relationship between each of these letters is as follows.

3. Pythagorean Number Sequential Generation Formula and Primitive Pythagorean Number Generation Formula

Let's review the Pythagorean number sequence generation formula [3], which was discovered by Tomatsumura, a former member of our laboratory.

There is another one known as the primitive Pythagorean number generation formula [4]. In summary, it can be explained as follows.

4. proof that perfect bricks cannot be created by primitive Pythagorean numbers

If the primitive Pythagorean numbers are given as the following.

At this time, there are natural numbers m and n (m>n), such that

Furthermore, the combination of primitive Pythagorean numbers such that

and α(diagonal), and the following equation is assumed to hold.

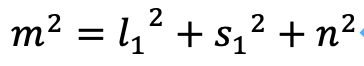
By repeating the same procedure, the following equation will be generated.

In other words, for a given α_n, the following equation holds.

Let's assume that for a rectangular face, the diagonals, short sides, and long sides are all natural numbers, and that the length of each is equal to the primitive Pythagorean number (l_n, s_n, s_(n-1)). By substitution, the following relation holds.

Since both sides are greater than zero

This is contrary to the fact that l_(n-1) and l_n are both natural numbers. (If they were both natural numbers, then the square root of 2 would not be an irrational number, which would be a contradiction.)

With the above method, we found that we cannot find a perfect bricks.

On the other hand, suppose that there exists a pair of primitive Pythagorean numbers such that β is diagonal. In this case, the natural number

exist and satisfy the following equation.

By the way, from the Pythagorean number continuous generation formula [3], l_1, s_1 and α make the following relation through β

On the other hand, there is also the following relationship for γ and α

From the above, we can see that through γ, l_1, s_1 and m, n have the following relationship

Let's transform this equation slightly.

Suppose that the right-hand side is

then it can be transformed as follows. We have set mn=l_1 so that we can complete the square.

But since the following,

l_1=s_1=1. From this result, we can also find the values of the natural numbers m and n, and we know that m=n=1.

We know from the result that l_1=s_1=1 that some piece of the triangle with β as the diagonal is zero. (Result 1)

We also know from the result that m=n=1 that α is zero. (Result 2)

Incidentally, when result 2 is true, result 1 is also true.

We found that we could not create a perfect bricks using the above method.

From the above, we know that it is impossible to create a perfect bricks using the primitive Pythagorean numbers. 5.

5) Proof that perfect bricks do not exist in general

Let's try to create a perfect bricks using general Pythagorean numbers. However, the triangle created by the general Pythagorean numbers is similar to the one created by the primitive Pythagorean numbers, so we get the same result as we discussed in chapter 4.

Again, if we try to create a perfect bricks without using the Pythagorean numbers, we will not be able to do so because the diagonal will be an impossible number.

From the above, it is impossible to create a perfect bricks using any combination of numbers.

6. conclusion

From chapter 4, we found out that we cannot create a perfect bricks from primitive Pythagorean numbers, and in chapter 5, we confirmed that we cannot create a perfect bricks from general Pythagorean numbers or any other numbers, so we know that there is no perfect bricks.