Proof of the Goldbach-Euler Conjecture

0. References

[1]http://www.tamagaki.com/math/Goldbach%27sConjecture.html "The Goldbach Conjecture"

1. What is the Goldbach-Euler Conjecture?

On 6/7/1742, Goldbach sent the following letter to Euler.

"Any natural number greater than five may be expressed as the sum of three prime numbers."

To which Euler replied

Euler replied, "Your conjecture can be rephrased as 'Any even number greater than 4 can be represented by the sum of two prime numbers.'" [1]

This explanation is given in detail in reference [1]. You can see how Euler is a genius.

Now, this is how the Goldbach conjecture was born, which generally states that "any even number greater than 4 will be represented by the sum of two primes. So while the equivalence proposition was first given by Goldbach, the form in which it is known today was created by Euler.

2. today's Olympics

We had the youngest gold medalist in Japan's history, Japanese placing first and third in those events, and two straight victories in judo! Basketball 3x3 is very interesting to me as a mathematician. I would like to discuss the potential energy depending on the position and the ability of the player, and the kinetic energy for the ball.

3. Proof

According to Goldbach's conjecture, for any even number

There is an odd prime number

such that

(An even number that is twice a prime number can of course be expressed as the sum of two primes.)

For any odd prime number,

there is some even number

that requires an error

to satisfy the following equality,

which results in the following equality relationship.

3.1 The case ε>0

For odd primes p and q, we use Bertrand Chebyshev's theorem.

(When n is an even number)

(when n is an odd number)

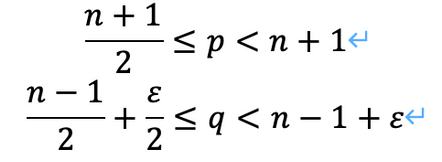
If we add each side, regardless of the evenness of n, we get

Equal sign establishment is as follows.

This contradicts ε>0.

Even if the equal sign does not hold, we still have

so that this is a clear contradiction from the fact.

3.2 The case of ε<0

Using a positive positive number ε'>0, satisfying ε=-ε', we can rewrite the following

Use Bertrand Chebyshev's theorem for odd prime numbers p and q.

(when n is an even number)

(when n is an odd number)

If we add each side, regardless of the evenness of n, we get

Comparing with the leftmost side, if the equality sign holds, then

This is a contradiction because p+q=0.

Even if the equality does not hold, we still have

so that this is a clear contradiction from the fact.

3.3 Summary

From the results of 3.1 and 3.2, we obtain the following result from ε = 0.

This result shows that the Goldbach-Eulerconjecture is correct.