n番目の素数を与える公式を満たすnについての定数関数かつ累乗の単位元となるe_E(n)について
- S Y
- 2022年4月30日
- 読了時間: 3分
0.参考文献
フィボナッチ数列について(その1) - フィボナッチ数列はどのようなものでどんな性質を有しているのか - ニッセイ基礎研究所
群について基本的なこと[物理のかぎしっぽ] 「可換群と非可換群・加群・乗群」
[3]https://ja.wikipedia.org/wiki/クヌースの矢印表記クヌースの矢印表現
1.フィボナッチ数に対する考察
1.1特性方程式と一般項[1]
フィボナッチ数を考えるとき、以下の特性方程式が役立ちます。

この解をα,β(α<β)とします。ちなみにβは黄金比φとなります。
この時、n番目のフィボナッチ数を与える公式(ビネの公式)は、以下のようになります。

2.二項演算表示
2.1表記法
可換群を満たす二項演算の代表例として、加群と乗群があります。[2]足し算を英語でAddition、掛け算を英語でMultiplicationというので、ここでは数aとbに対する足し算を
A(a,b)=a+b
掛け算を
M(a,b)=a*b
と表すことにします。
可換群を満たさない二項演算の代表例として、累乗群を考えることができるでしょう。累乗を英語でExponentationと言いますので、aのb乗をここでは
E(a,b)=a^b
と表すことにします。
さて、A,M,Eの演算はそれぞれ以下の関係となっています。
a+a+a+...をb回→M(a,b)
a*a*a*...をb回→E(a,b)
このように、二項演算を有限回行うことで、別の二項演算を考えることができます。
この類推から、以下の演算も考えられます。ただしE(a,b)から類推したので、この演算による群は非可換群となります。
a^a^a^...をb回→a↑↑b→T(a,b)
矢印を用いた表記はクヌースの矢印表記と言います。また、T(a,b)はTetrationと言いますので、Tを用いました。[3]
2.2 単位元
ある二項演算F(a,b)に対して、単位元eが存在することがあり、
F(a,e)=F(e,a)=a
を満たします。例えば、足し算では0が、掛け算では1がそれぞれ単位元となります。
2.3 逆元
2.3.1 一般例
ある二項演算F(a,b)に対して、数aに対する逆元a^(-1,F)が存在することがあり、
F(a,a^(-1,F))=F(a^(-1.F),a)=e_F
を満たします。例えば、足し算では数aに対して-aが、掛け算では数aに対してa^(-1)がそれぞれ逆元となります。
2.3.2 E(a,b)の逆元
E(a,b)の演算は非可換ですから、単位元と呼べるものは本来ありません。しかし、便宜上、数nに対する定数関数として、単位元e_Eを与えることにします。
すると、ある数xに対して逆元y

を考えることができます。加群と乗群で、逆元はある数xに依存する値であったので、y=y(x)であるべきだと考えられ、非自明解を採用することにします。
3.フィボナッチ数の特性方程式と一般項を、二項演算表示してみる。
特性方程式は、

であり、一般項は、

となります。
4. 素数の一般項を与える
演算が次のように小さい順にレベル分けされているとします。
A < M < E < T
フィボナッチ数が足し算を基としていたことを踏まえて、素数は掛け算にレベルが上がったと捉えて、ひとつずつ上げていきましょう。
4.1 特性方程式
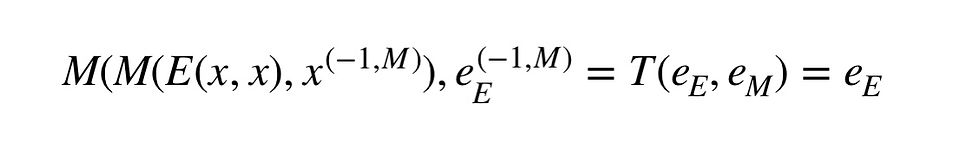
この式を、通常の書き方に直すと次のようになります。

ここで定義より、e_E^2=2となります。計算すると、xは、フィボナッチ数の特性方程式と同様に、2重解となり、

となります。
4.2 素数の公式を与えるe_Eについて

この式を、通常の書き方に直すと次のようになります。

では、実際にこの数式が機能する様に、e_Eを求めてみましょう。(すなわち、nとe_Eの相関関係を調べます)ただしf(n)=1とします。
表から、e_Eはネイピア数(又はオイラー数)、e=2.71828…に近づくことがわかりました。しかし、残念ながら十分大きな数で成り立つかは不明であり、またテトレーションはコンピュータの計算能力では到底処理できないので、真偽の程は分かりません。ですから、次の予想を考えることができます。
自然数nとn番目の素数f(n)は以下の関係式で表せ、かつe_E=e=2.71827…だろう。
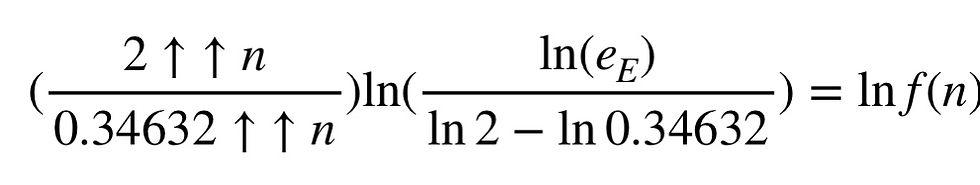




コメント