Conjecture for the interval of prime numbers

[1] Assertion of the prediction

The following equation is true. And they are all equivalent.

The upper equation: Equation 1-1 The middle equation: Equation 1-2 The lower equation: Equation 1-3

5<p<q<r: odd primes

In other words, we argue that any prime number will be bounded by the sum of the two largest primes that are smaller than itself.

An example is summarized in the table below.

Figure 1-1

Incidentally, when (p,q,r)=(3,5,7), Equation 1-1 is clearly valid.

[2] Proof of the equivalence of equations 1-1 and 1-3 (1)

Assume that the following equations are satisfied simultaneously.

Top: Equation 2-1 Bottom: Equation 2-2

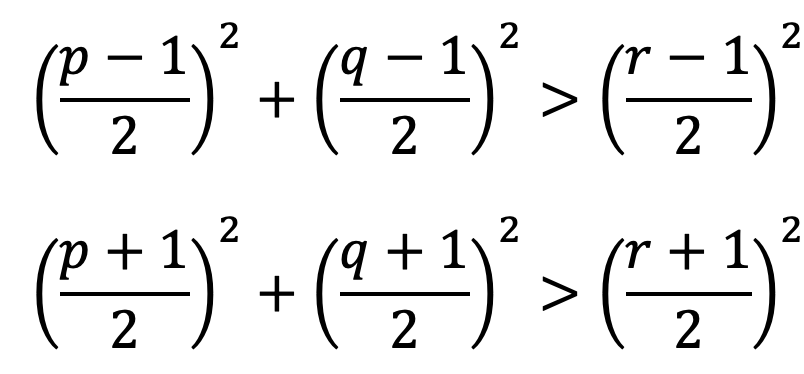
If we add up the two sides and sort it out.

Equation 2-3

where p, q, and r are all odd numbers, so if we take care of the even-odd

Equation 2-4

It becomes

Now, consider the following complementary problem.

Now, for Eq. 2-1 and Eq. 2-2, ε_1 and ε_2 are

Therefore, the condition is satisfied. Subtracting each of the two sides, we get

It goes like this.